01 绪论
"The art of doing mathematics is finding that special case that contains all the germs of generality."
“数学之道在于找出一个这样的特例,它包含普遍原则的全部萌芽。”
面积问题
圆的面积公式:S = \pi R^2,但他从何而来?
思考这个问题有助于窥见微积分的三个中心思想:积分,微分,以及两者互逆
当估计圆的面积时,你可能将圆切成更小的部分,其面积更容易近似,然后将结果相加。每种切法都可能导致自己有趣的推理路线。
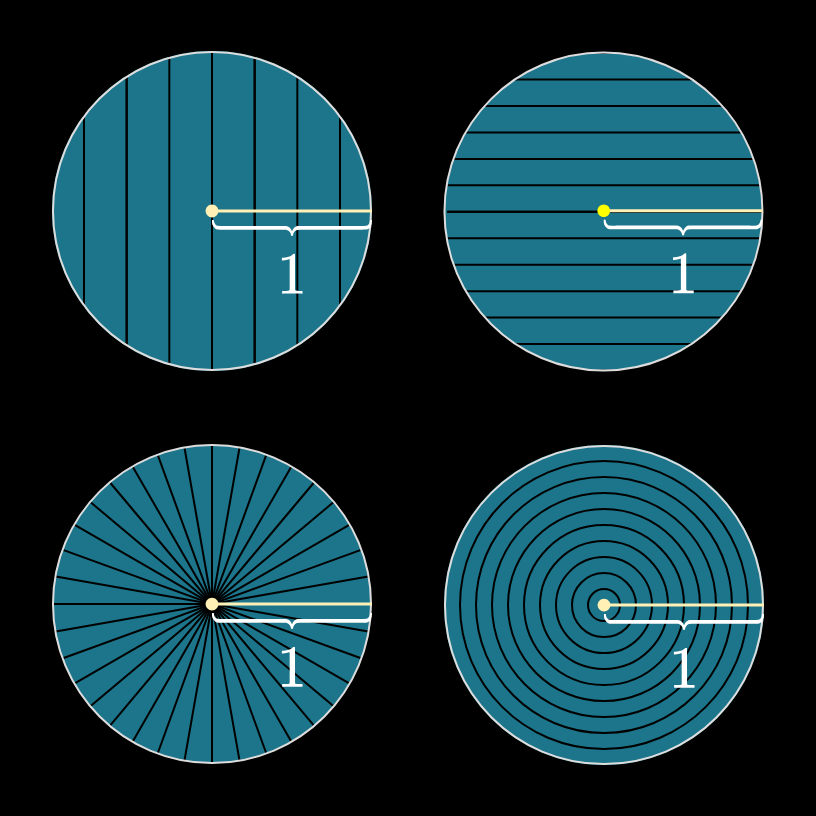
当你尊重对称性时,数学倾向于奖励你,所以在上面显示的划分中,无论是左下角的划分成披萨片,还是右下角的划分成同心圆环,都可能会引导我们走上一条富有成效的道路。现在,让我们考虑一下同心环的划分.
解开同心环
取其中一个圆环,其半径 r在 0 到 1 之间。厚度为 \mathrm{d}r(为体现微积分标准符号的思想),表示从一个环到下一个环的半径的微小差异。
通过求得每个圆环的面积,在做叠加,便可得到整个圆的面积。
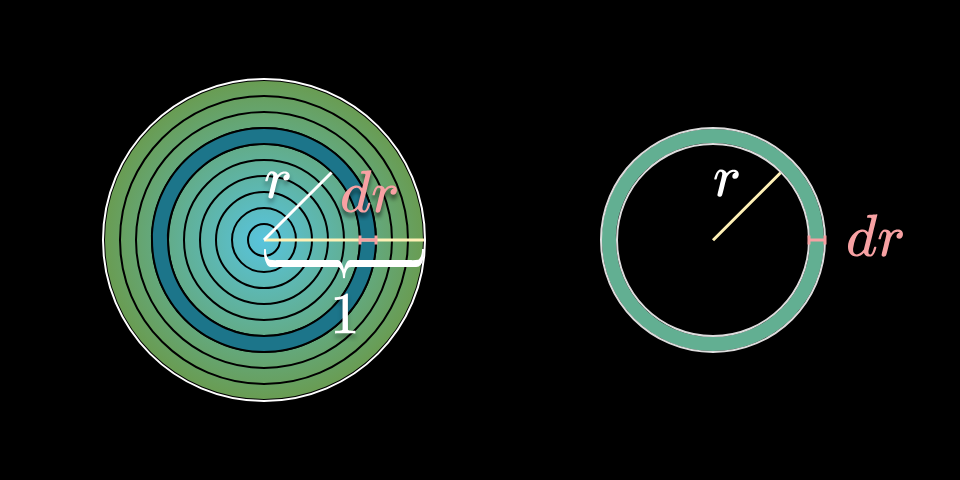
我们不妨将其拉直,并将其近似于矩形(长 2 \pi r,宽\mathrm{d}r)。这个矩形的面积是 S = 2 \pi r \ \mathrm{d}r
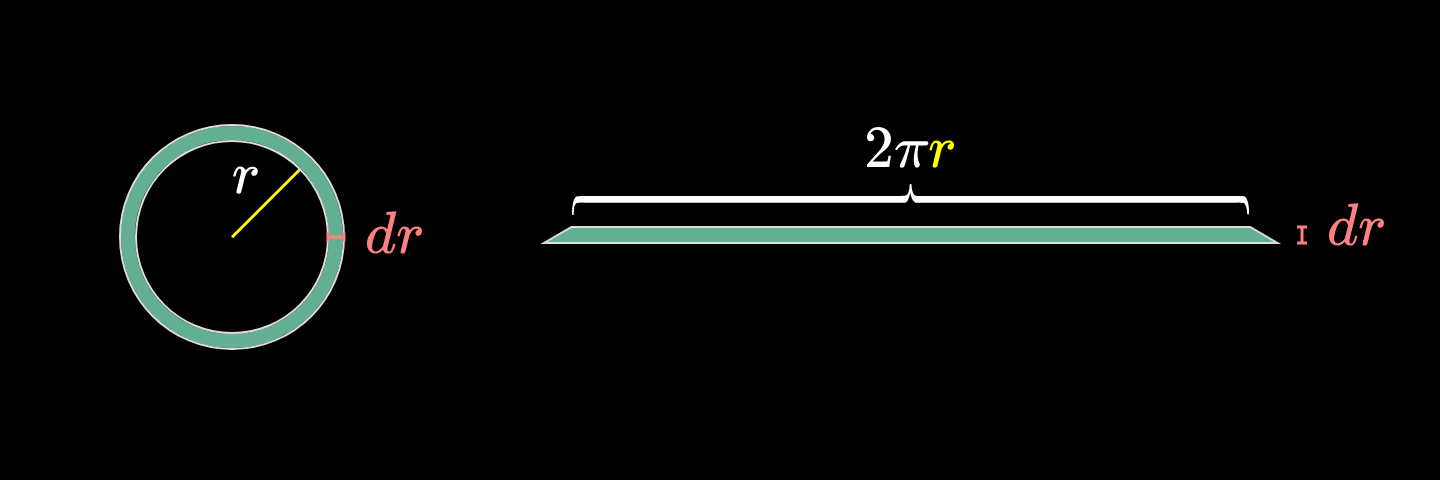
尽管我们选择的矩形和其实际形状(梯形)之间有一些面积差距,但当\mathrm{d}r越来越小时,这个提醒上下两条边将愈发趋近于统一长度,该面积误差也将越来越小。
制图
环的内半径大小范围从最小的环为 0 到最大的环为 1-\mathrm{d}r,两两之间相差我们选择的任意厚度间隔\mathrm{d}r,例如 0.1 。 但随着\mathrm{d}r变小, r的上限越来越接近 1 。
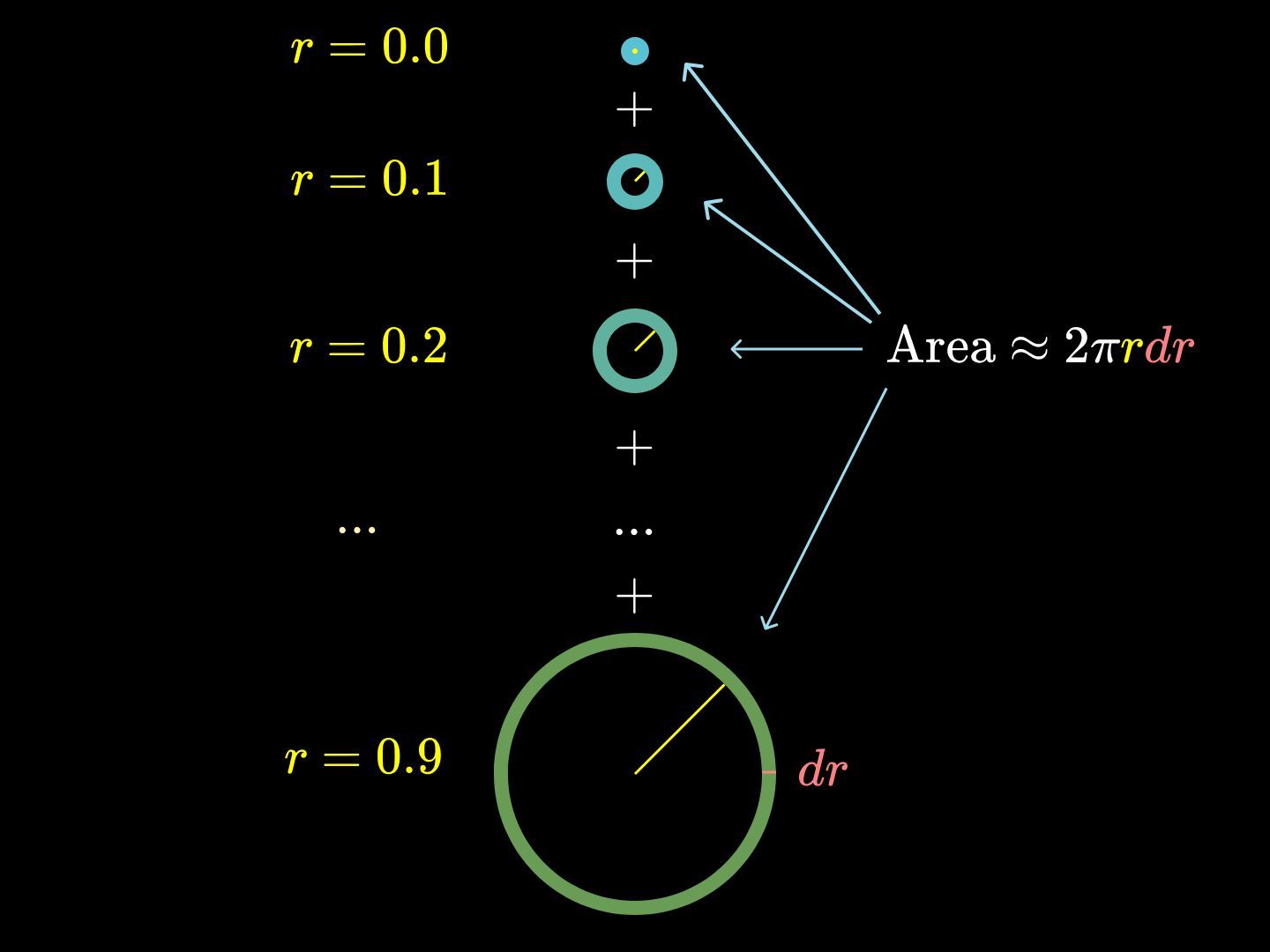
为考虑这些近似了圆环面积的矩形
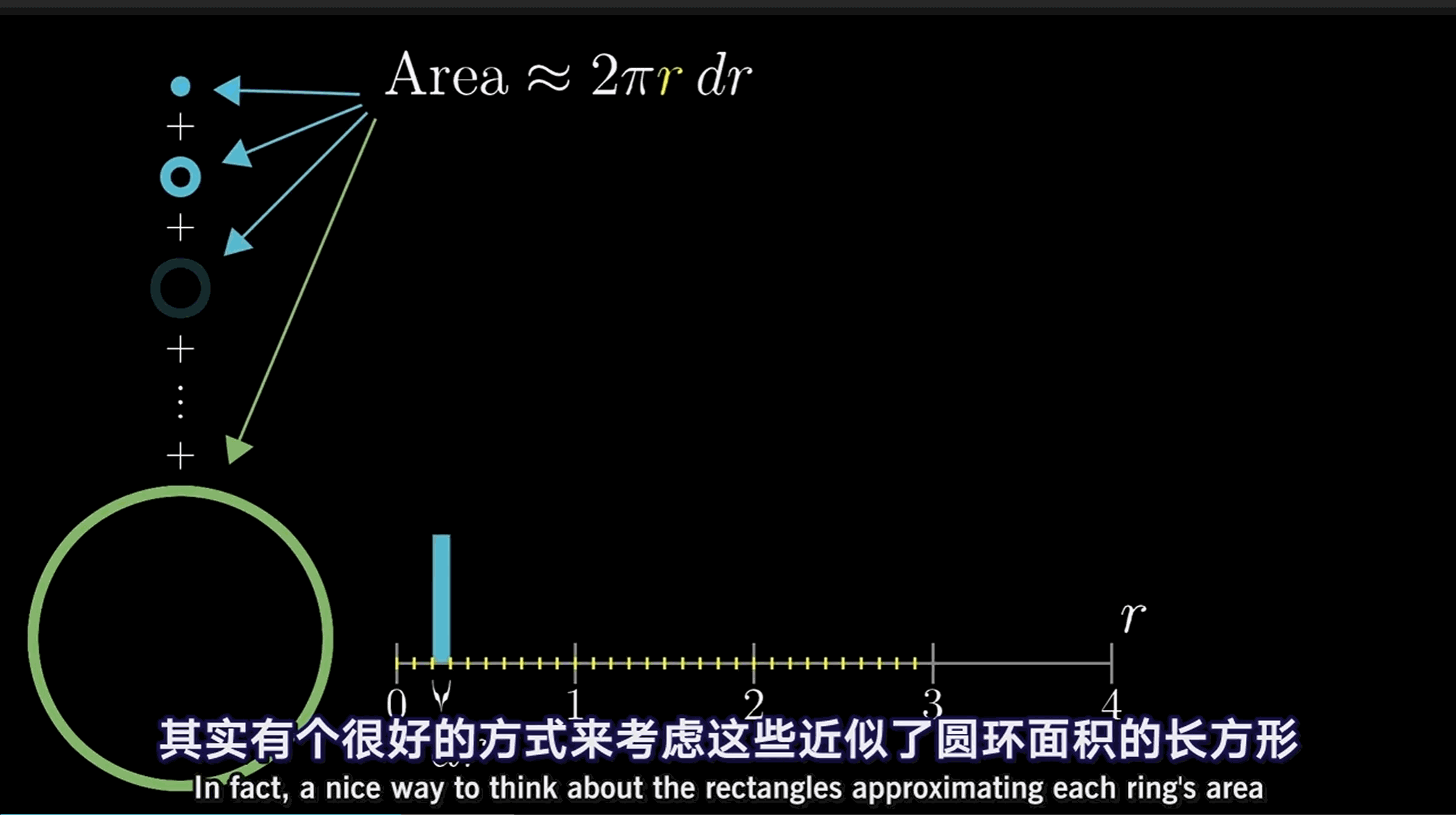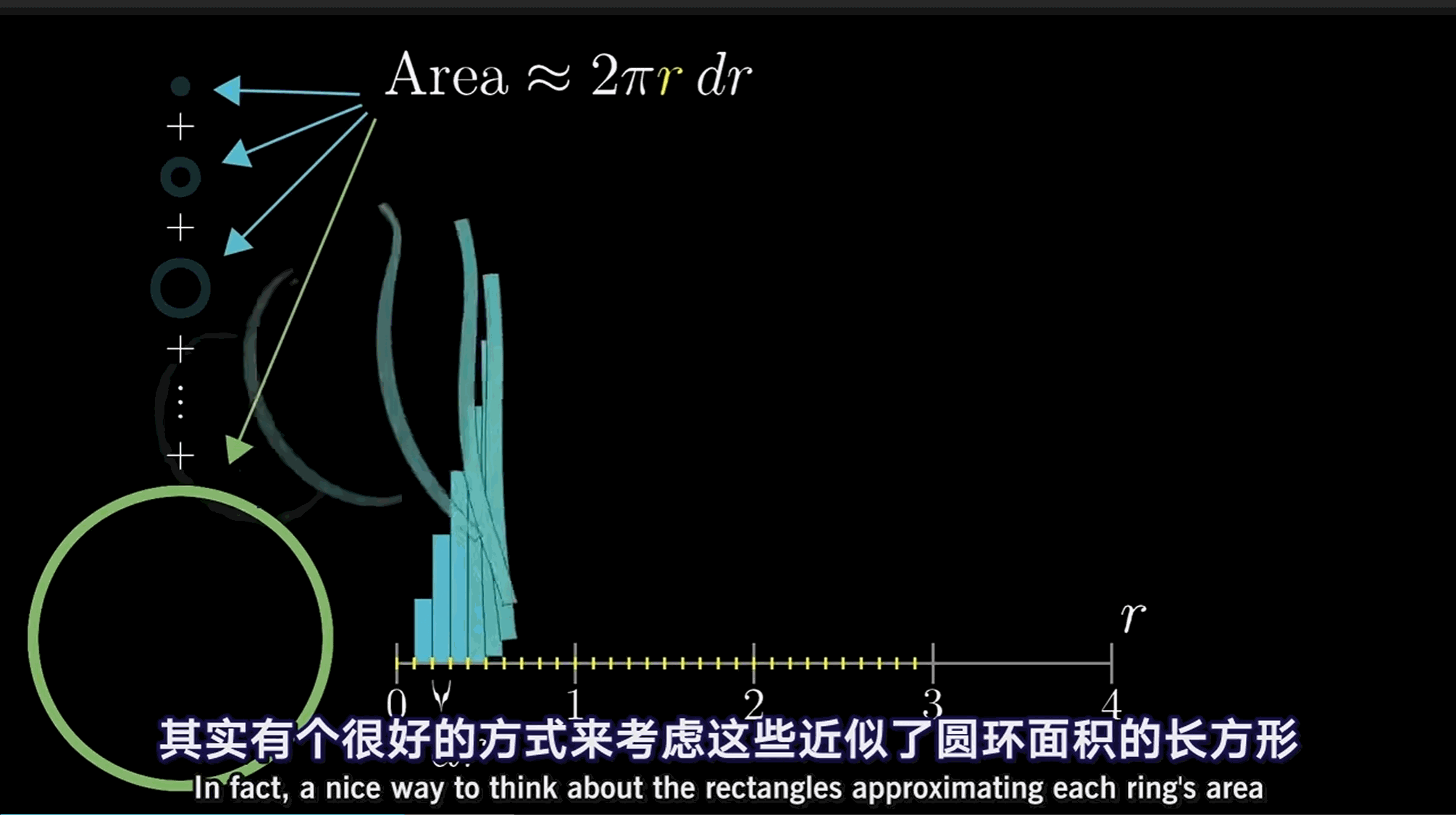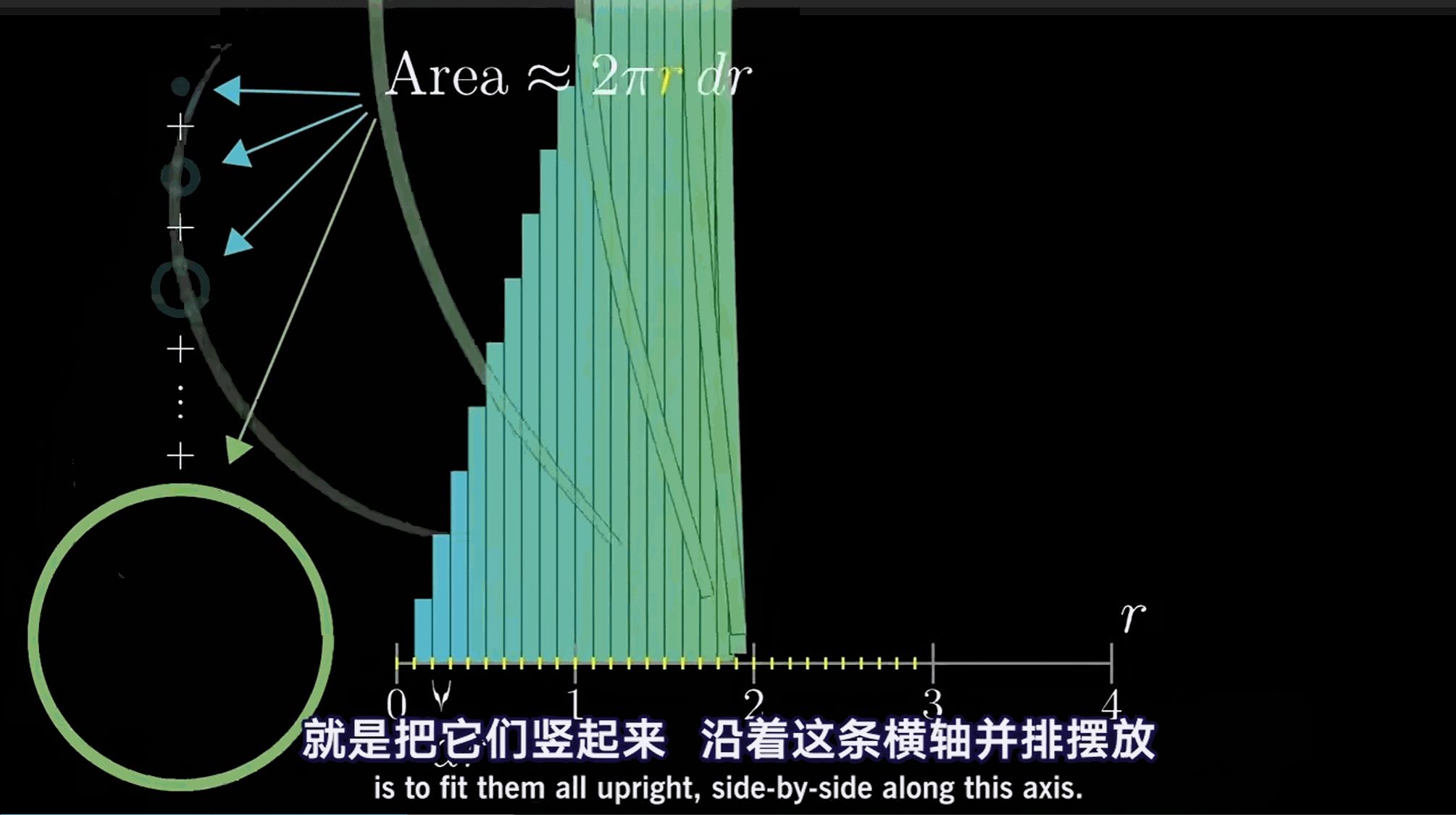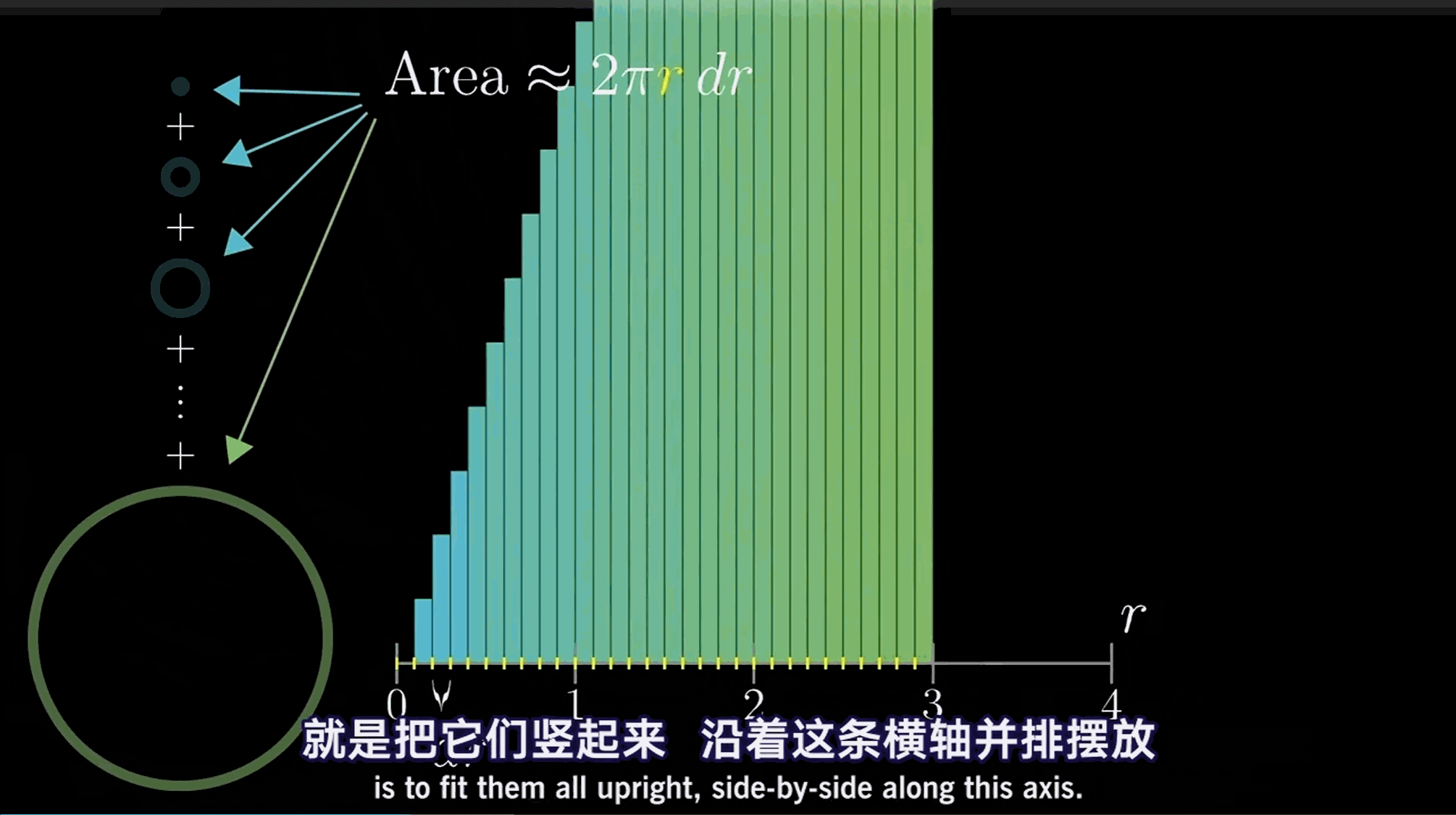
每一个的厚度都是\mathrm{d}r,且对于每一个r的取值,位于其上长方形的高均为2 \pi r。
考虑此布局的方法是绘制2 \pi r的函数图像,即这条斜率为的直线。每个矩形都伸展到刚好碰到这条直线。
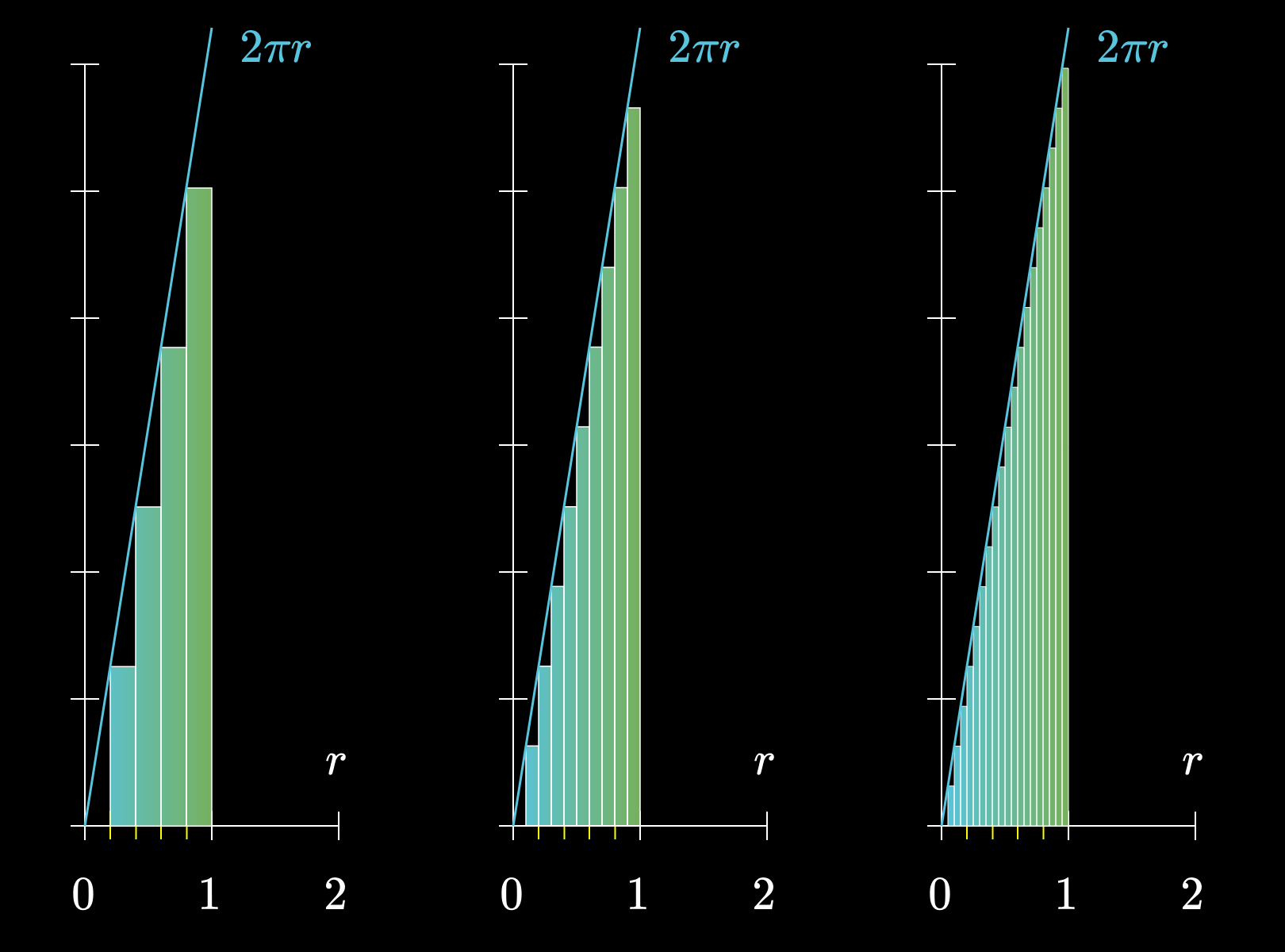
当\mathrm{d}r越来越小时,矩形面积之和也与三角形面积相差越来越小。因此我们仍然可以用三角形面积近似所有矩形面积之和。
三角形的底是 1,高是2\pi \cdot1。因此,三角形面积是S =\dfrac{1}{2}\cdot 1\cdot(2\pi \cdot1)=\pi\cdot1^2。
或者,当我们原始圆的半径是其他值R时,则该面积将是S=\dfrac{1}{2}\cdot R \cdot (2\pi R)=\pi R^2。
这就是圆的面积公式。
积分
将上述方法抽象可以得到如下流程图,这是解决数学中许多难题的通法。
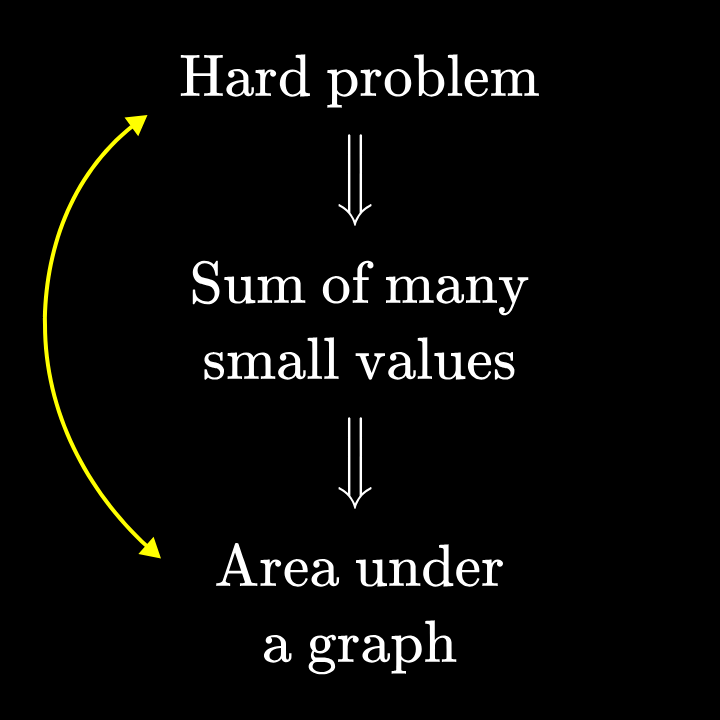
例如,如果你想根据汽车在每个时间点的速度计算出它行驶了多远,你可以在许多时间点上测距,并将每次的速度乘 tt 以一些微小的时间 dtdt 变化,以得到相应的在短时间内行驶的距离。
并将其
